sum $ take 20 $ snd <$> iterate (\(n,x) -> (n+1, x/n)) (1.0, 1.0) sum $ take 20 $ snd <$> iterate (\(n,x) -> (n+1, x*n/(2*n+1))) (1.0, 2.0)
Napier’s Constant
I had always been bothered by the origin story of the constant \(e\). Even a child can understand the constant \(\pi\), ratio of a circle’s circumference to its radius. In contrast, I imagine I’d have a tough time explaining the base of the natural logarithm to less mathematically inclined adults, let alone children.
We can express \(e\) as the sum of the reciprocal of the factorials:
\[ e = 1 + \frac{1}{1} + \frac{1}{1\cdot 2} + \frac{1}{1\cdot 2\cdot 3} + … \]
And \(\pi\) has a similar expansion:
\[ \frac{\pi}{2} = 1 + \frac{1}{3} + \frac{1\cdot 2}{3\cdot 5} + \frac{1\cdot 2\cdot 3}{3\cdot 5\cdot 7} + … \]
Both series converge quickly enough for cute party tricks:
You would think a constant with a simple elegant formula would have an easy explanation. This is indeed true for \(\pi\). Might this also be true for \(e\)? Did I somehow miss an easy explanation all these years?
To answer this question, I read e: The Story of a Number by Eli Maor, which comprises of seemingly unrelated episodes, each culminating in a big reveal where we learn \(e\) was behind it all along. For example:
-
John Napier, the 8th Laird of Merchiston, "doubled the life of the astronomer" by publishing a table of numbers capable of miracles such as transforming multiplication into addition, division into subtraction, and taking square roots into halving.
-
For the same rate, interest compounded daily grows faster than interest compounded monthly. What do we get when it is compounded more frequently? What if it were compounded continuously?
-
Even before calculus, mathematicians managed to measure the area under curves of the form \(y = x^n\) where \(n\) is an integer. The toughest case is \(n = -1\), the hyperbola. Why? And what’s the answer?
-
Calculus gave mathematicians a brand new toy to play with, who promptly tried it on curves like \(y = 2^x\). They found its derivative was \(y' = m 2^x\) where \(m\) is the slope of the curve at \(x = 0\). Does this mean for some \(r\), the slope of \(y = r^x\) at \(x = 0\) is exactly 1, yielding a function that is its own derivative?
The fourth puzzle was how I first learned about \(e\), from a calculus textbook whose title I forget. I learned of the other 3 puzzles soon after, so I hadn’t missed out after all.
In other words, the bad news is \(e\) is not as easy as \(\pi\). But the good news is we get to watch a gripping drama. When young, we enjoy simple stories, but as we age, we are drawn to mysterious and intricate plots with interwoven threads, often presented nonlinearly.
Maor tells a good tale, and his book is full of tasty historical tidbits, but he botches the opening scene. He distorts Napier’s contributions. Maor’s statement in footnote 13 of the first chapter, "The often-made statement that Napier discovered [\(1/e\)] (or even \(e\) itself) is erroneous", is itself erroneous.
Instead of a documentary, we’re left with a yarn based on a true story. We set the record straight, with the help of Denis Roegel, Napier’s ideal construction of the logarithms.
An unjust twenty-year sentence
Maor claims Napier built his wonderful canon of logarithms by choosing the following base, or common ratio:
\[ 1 - 10^7 = 0.9999999 \]
Maor suggests Napier then computed successive powers until he reached 0.5. This cannot be! It already takes over a million iterations to reach 0.9:
length $ takeWhile (> 0.9) $ iterate (0.9999999*) 1
Indeed, Maor corrects himself when he lists the geometric progressions that Napier actually computed. They come in 4 flavours:
-
Napier did in fact compute successive powers of \(0.9999999\), but only one hundred of them: \(1, 0.9999999, …, 0.9999999^{100}\).
-
He computed successive powers of a five 9s version of the ratio: \(1, 0.99999, …, 0.99999^{20}\).
-
He computed successive powers of a two 9s version of the ratio: \(1, 0.99, …, 0.99^{68}\).
-
For every \(c\) in the previous step, he computed \(c, 0.9995 c, …, 0.9995^{20} c\).
Maor states: "…he set himself to the task of finding, by tedious repeated subtraction, the successive terms of his progression…Napier carried it through, spending twenty years of his life (1594-1614) to complete the job."
Really? We’ll examine the details later, but briefly, the first three sequences only require shifts and subtractions, while the sequences of the last step require only a little more work in the form of one extra halving operation.
The total bill comes to 1568 shifts and subtractions, and 1380 halvings.
100 + 20 + 68 + 69*20 69*20
Throughout my school years, my teachers frequently assigned around 10 homework exercises that were due the next day: exercises comparable in technical difficulty to subtraction and halving. (Some exercises may have revolved around more advanced concepts like integration, but the calculation itself followed simple rules.) In other words, schoolchildren could complete these tables within half a year! There is no way Napier needed twenty. Maor’s sentence must be false.
And what could Napier possibly have done with these sequences? All numbers of the first two sequences are close to 1, and there are only about 120 different numbers anyway. The numbers of the third sequence are the seeds for the last set of sequences, which are numerous and range from 0.5 to 1. The latter must be where Napier looked up numbers to find their logarithms. This should raise alarm bells. Two different sets of alarm bells, for we have exposed two gaping plot holes.
Firstly, if Maor’s explanation is to be believed, it appears the ratio Napier used was not 0.9999999 but rather 0.9995.
Secondly, and more worryingly, what is the point of the first three sequences? If Napier had chosen the ratio 0.9995, then all he had to do was compute:
\[ 1, 0.9995, …, 0.9995^{1386} = 0.49998… \]
namely, one sequence of 1387 numbers instead of 69 sequences with 21 numbers each. There must be more to the story.
Waiting for Zeno
To truly understand Napier, we should walk a mile in his shoes. We do so almost literally, because Napier explained logarithms by imagining a point traveling a certain distance in a straight line that periodically marked off distances following a geometric progression.
It seems Zeno was his cobbler because allowing artistic license, the trek Napier envisioned began at noon at one mile per hour, but slowed down exponentially as the destination neared. Every hour on the hour, the remaining distance is \(r\) times the remaining distance one hour ago, for some constant \(r < 1\). We’ll never arrive, despite getting arbitrarily close.
Let’s take advantage of modern mathematical notation to analyze this journey. For a natural \(n\), let \(f(n)\) be the remaining distance in miles after \(n\) hours. Thus:
\[ f(0) = 1 , f(n + 1) = r f(n) \]
By induction:
\[ f(n) = r^n \]
Let’s extend this equation to all reals \(t\):
\[ f(t) = r^t \]
Initially, we head towards our destination at one mile per hour:
\[ f'(0) = -1 \]
Haven’t we met somewhere before? This is the fourth puzzle listed above, namely, how I first learned \(e\) decades ago from my calculus textbook, except with a sign flipped. We must have \(r = 1/e\).
Napier defined the logarithm to be the inverse of \(f\): given a remaining distance in miles, how many hours have elapsed? In other words, Napier invented logarithms to the base \(1/e\).
Maor alleges: "Napier unknowingly came within a hair’s breadth of discovering" \(e\).
Let’s take stock. Napier defined the same function (up to sign) that my calculus textbook defined to introduce \(e\), a function that Maor himself discusses in Chapter 10. For memory, my textbook only argued \(e\) was between 2 and 3, and stated several digits without proof. In contrast, Napier figured out quite a few digits of quite a few numbers, and explained how he did it. In his 1614 table, the entry for 21 degrees and 35 minutes includes:
3678541 1000685
This means Napier is claiming \(\ln 0.3678541 = -1.000685\), which is startlingly accurate: only the last digit is wrong. We can interpret this as:
\[ 1/e \approx 0.3678541 \]
which is correct to 4 decimal places (\(1/e = 0.3678944…\)).
Napier even saw that the remaining distance (in miles) is also the current speed (in miles per hour), a fact his work hinged on. This is obvious today because we all know the derivative of \(e^t\) is itself, but Napier had no access to calculus. In fact, in his day, non-integer exponents were poorly understood.
Is it fair, then, to say Napier only came close to discovering \(e\)?
Confusingly, in Appendix 1, Maor mentions Napier’s moving point, and adds: "Napier’s logarithms are actually logarithms to the base \(1/e\)", contradicting his Chapter 1 claim that after rescaling, the base is \( (1 - 1/10^7)^{10^7} \).
The retconning of Appendix 1 somewhat redeems Chapter 1, but still fails to explain why Napier bothered computing the first three sequences. It also introduces another gun that Chekhov would condemn. If Napier’s goal was to compute successive powers of 0.9999999, why did he define this moving point?
We’ll soon reveal the terrifying reasons, but first we atone for some storytelling transgressions.
A Pointless Exercise
We’ve swept a couple of details under the rug. My guess is Napier wanted a function that takes a length and returns a length, so he wrote of a second point that always moved at 1 mile per hour, and defined the logarithm using the distance traveled by this second point. We view this as an unnecessary layer of indirection.
More troublesome for us was that Napier lived through a sort of numerical hyperinflation. A cutting-edge researcher, Napier was at ease with the latest inventions such as the decimal point: indeed, Napier helped popularize this handy spot of notation. But in 1614, for the sake of his intended audience, he chose a sinus totus of \(10^7\), pumping up his numbers by 7 zeroes (markedly fewer than the number of zeroes tacked onto certain unfortunate currencies throughout history).
Instead of "0.1234567", readers would see "1234567", with no trace of those newfangled decimal points. They’d have to rescale now and then, but this was a prevailing custom anyway.
In detail, the Naperian logarithm is given by:
\[ \newcommand{\NapLog}{\mathop{\rm NapLog}\nolimits} \NapLog x = - 10^7 \ln (x / 10^7) \]
We do our best to dodge this security-blanket scaling factor, though if we replace "mile" with "sinus totus" then some of our statements are equivalent to Napier’s. But on occasion we really are talking about numbers ten million times smaller than Napier’s.
One particularly tiresome mismatch is that \(\NapLog 10^7 = 0\). Everybody loves that:
\[ \log a b = \log a + \log b \]
but with Naperian logarithms, we get:
\[ \NapLog a b = \NapLog a + \NapLog b - \NapLog 1 \]
Naturally, Napier’s fans soon clamoured for an upgraded logarithm that returns 0 when given 1.
Shift Work
Let’s look closer at the calculations Maor describes, which supposedly took 20 years. We call them auxiliary tables, but fear not: we’ll soon divulge their true purpose.
When multiplying a number \(x\) by a number of the form \(1 - 10^{-n}\), Napier shifted \(x\) right by \(n\) places, simply truncating digits to fit into the desired precision.
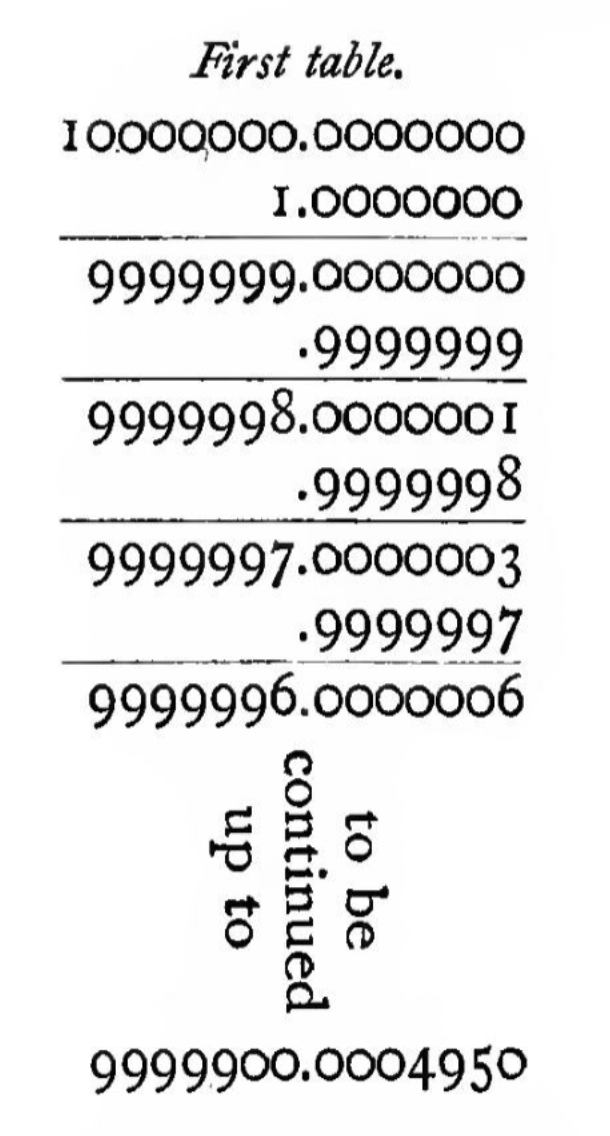
Napier computed his first sequence with 14 decimal places of precision. The common ratio is \(1 - 10^{-7}\).
aux1 = take 101 $ iterate (\n -> n - n `div` 10^7) (10^14) take 5 aux1 last aux1
We stick to integer arithmetic to make it clear where the truncation occurs. (So now we’re the ones avoiding decimal points with hyperinflation!)
Our digits agree with Napier’s:
Napier used 13 decimal places for the second sequence, whose common ratio is \(1 - 10^{-5}\).
aux2 = take 51 $ iterate (\n -> n - n `div` 10^5) (10^13) take 5 aux2 last aux2
This time we disagree with Napier:

The first 5 numbers are identical, but the last digits of the last number should be 4826, not 2927. Napier must have slipped up at least once along the way. We’ll soon witness this tiny bug spread and grow as Napier computed more of his logarithms.
For the heads of the 69 sequences, Napier used 11 decimal places. The common ratio is 0.99:
aux3heads = take 69 $ iterate (\n -> n - n `div` 100) (10^11)
The rest of each of these sequences have the common ratio of 0.9995, which some sources say were computed by shifting, then halving, then subtraction. I assume Napier also truncated digits for these shifts, but what about the halving? Did he truncate? Or did he round? Did he actually use higher precision then truncate later? Could he have halved before shifting?
Whatever he did, I was unable to reproduce it exactly. We choose to shift, truncate, halve, round, then subtract:
aux3 = map (take 21 . iterate (\n -> n - (n `div` 1000 + 1) `div` 2)) aux3heads aux3sample = (take 3 aux3 ++ [last aux3]) (\ns -> (take 5 ns, last ns)) <$> aux3sample
This gets us pretty close:

Luckily, the discrepancies only seem to affect the last digit, and at any rate they have far less impact than Napier’s mistake in the second auxiliary table.
The War on Error
Napier must have realized the accumulated truncation error bound grows linearly with each step. This may be why he chose 69 sequences with 21 items each rather than a giant sequence with over 1000 truncations. Within each of the 69 sequences, an entry has at most 20 accumulated truncation errors.
The start of the 69th sequence, 50488588900, is off by at most 63; less than 68 because it comes from a sequence with a ratio of 0.99 computed with 11 decimal places, so the first 5 shifts and subtractions are exact. With arbitrary precision arithmetic at our fingertips, we find the last 3 digits should be 878, not 900:
take 11 $ show $ 99^68
Maor suggests that Napier took the index of an entry to be its logarithm. Not so. Napier only computed the 69 sequences to establish geometric progressions with reasonable coverage of the interval [0.5..1]. Then the real fun begins: Napier proceeds to compute the logarithms of each member of each progression.
Why not just use an entry’s index? Because Napier cared deeply about accuracy (aside from the last few digits lost to truncation errors). He knew no power of 0.9995 is exactly 0.99, so integer indices won’t cut it.
There’s more. For the sake of argument, let’s say Napier somehow possessed accurate approximations to some logarithms, for example:
\[ 0.9995^{1349} = 0.5093251… \]
\[ 0.9995^{1350} = 0.5090704… \]
Then how do we solve the following?
\[ 0.9995^x = 0.5092 \]
The answer lies between 1349 and 1350, but where exactly? Should we linearly interpolate and hope for the best?
I speculate Napier may have toyed with ideas like this. But in the end, Napier did the right thing: define a sort of continuous ideal geometric progression, namely the exponential curve, and exploit its properties to produce incredibly accurate approximations.
By the way, Napier of course computed Naperian logarithms, but we speak of natural logarithms instead. One might object that we need \(\ln 10\) to convert one kind to the other, but this constant is unneeded when computing Naperian logarithms alone, and once done, we can figure out \(\ln 10\) from the tables.
I got 0.99 problems
The properties of logarithms imply a shortcut. If Napier could look up the values of \(\ln 0.99\) and \(\ln 0.9995\) then he could just add and subtract to find the logarithms of all \(69 \times 21\) numbers in his coverage table, the third auxiliary table. Unfortunately, his goal was to create from scratch a lookup table that would provide such answers in the first place! We have a chicken-and-egg problem.
It is only at this point we learn why Napier bothered with the first two sequences. They were for bootstrapping:
-
Napier found a good approximation for \(\ln 0.9999999\).
-
Since \(0.9999999^{100} \approx 0.99999\), their logarithms are also close. Napier bounded the difference between their logarithms to approximate \(\ln 0.99999\).
-
Since \(0.99999^{20} \approx 0.9995\), their logarithms are also close, but this time, instead of bounding their difference to derive an approximation, he went above and beyond. He approximated the logarithm of their ratio using the highly accurate approximation from step 1, which in turn led to an approximation for \(\ln 0.9995\).
-
Since \(0.9995^{20} \approx 0.99\), their logarithms are also close. Napier found an approximation for \(\ln 0.99\) in a similar manner as the previous step.
-
Profit! Napier approximated the logarithms of every number in his lookup table via repeated additions of the approximations for \(\ln 0.99\) and \(\ln 0.9995\).
Napier’s moving point makes short work of step 1. When there are 0.9999999 miles left to go, our current speed is also 0.9999999 miles per hour. Our pace was only faster in the past, which means we took less than \( (1 - 0.9999999) / 0.9999999 \) hours to reach our current position.
Dually, since we set off at 1 mile per hour, and since our pace has only slowed, more than \( 1 - 0.9999999 \) hours have elapsed. In other words:
\[ 1 - 0.9999999 < -\ln 0.9999999 < \frac{1 - 0.9999999}{0.9999999} \]
Napier approximated the denominator of the right-hand side with the first few terms of the geometric series:
\[ \frac{1}{1 - 10^{-7}} = 1 + 10^{-7} + 10^{-14} + … \]
and averaged the resulting bounds to get:
\[ \ln 0.9999999 \approx -1.00000005 \times 10^{-7} \]
This agrees with Google, and any program limited to IEEE 754 double-precision floats. We need more precision to detect the error:
\[ \ln 0.9999999 = -1.00000005000000333333358… \times 10^{-7} \]
Napier took the first 100 multiples of -1.00000005 to be the logarithms of the (approximiate) powers of 0.9999999. In particular, his first sequence ended with:
\[ 0.9999999^{100} \approx 0.9999900000495 \]
thus:
\[ \ln 0.9999900000495 \approx -1.00000005 \times 10^{-5} \]
In general we have:
\[ x < -\ln (1 - x) < \frac{x}{1 - x} \]
which may look banal to modern eyes, because of the Taylor expansion:
\[ -\ln (1 - x) = x + \frac{x^2}{2} + \frac{x^3}{3} + … \]
So we stress Napier derived these bounds without calculus, for a brand new function he invented. Napier provided no explanation for choosing the average, but we can see it’s essentially the second-order Taylor approximation.
What’s the difference?
If we replace \(1 - x\) with \(a/b\) and rearrange, we obtain:
\[ \frac{a - b}{b} < \ln b - \ln a < \frac{a - b}{a} \]
Napier used this formula to approximate a logarithm if he already knew a nearby logarithm. For step 2, set:
\[ a = 0.9999900000495, b = 0.99999 \]
The bounds on either side are approximately:
\[ a - b = -4.95 \times 10^{11} \]
so he took the lower and upper bound to be the same. Thus:
\[ \ln 0.99999 \approx \ln 0.9999900000495 - 4.95 \times 10^{11} \approx -1.000005 \times 10{^-5} \]
Again, this agrees with double-precision float arithmetic, and we need higher precision to spot the error.
While not obvious in this particular case where the upper and lower bounds are identical, Napier performed interval arithmetic, that is, he postponed the averaging of bounds as late as possible. He added lower bounds together and upper bounds together, and only when he wanted to record a single number would he compute their mean.
Then we have the beginnings of a tragedy. Napier’s erroneous last few digits in the last entry of the second auxiliary table, 2927 instead of 4826, means the following approximation is worse than it should have been:
\[ \ln 0.99999^{50} \approx 50 \times \ln 0.9995001222927 \approx -5.000025 \times 10^{-4} \]
The bug propagates in step 3, where Napier computed:
\[ \frac{0.9995}{0.9995001222927} \approx 0.9999987764614 \]
Setting:
\[ a = 0.9999987764614, b = 0.9999999 \]
in the above leads to:
\[ \ln 0.9999987764614 \approx -1.2235387 \times 10^{-7} \]
then interval arithmetic and averaging yields:
\[ \ln 0.9995 \approx \ln 0.9999987764614 - \ln 0.9995001222927 \approx 5.0012485387 \times 10^{-4} \]
This approximation is smaller than it should have been because of Napier’s bug.
Step 4 followed a similar procedure to arrive at:
\[ \ln 0.99 \approx 0.1005033210291 \]
which again is lower than it should have been, because of other approximations that were infected by the bug.
Step 5 completes the tragedy. The error virulently spread and magnified throughout the third \(69 \times 21\) table, accumulating with every addition.
While the errors were tolerably small in practice, it is a shame that Napier worked so hard to boost accuracy but was sabotaged by a trivial mistake in elementary arithmetic.
To recap, Napier computed the first two sequences to determine approximate logarithms for the third table, and he invented the exponential function because the indices alone are far too inaccurate for approximating logarithms from known nearby logarithms.
However, we have not quite fired all the guns of Chekhov. How long would the above taken? Almost all of the logarithms are derived from others via addition or multiplication by a small constant. Only 4 of the logarithms require interval arithmetic. The divisions in the bounds can be approximated by multiplications with a truncated geometric series because the denominators are close to 1.
Overall, while it is certainly a mountain of work, it’s not an order of magnitude more than the initial shifts, subtractions, and halvings. It still would not have taken Napier twenty years.
What could have eaten so much time? Surely Napier spent hours on failed experiments and inferior approaches, and on finding miraculous coincidences such as \(0.9999999^{100} \approx 0.99999\), inventing the exponential function and interval arithmetic, and so on. But this kind of work is not soul-crushing drudgery.
The bulk of the two decades must have been spent elsewhere.
Take care of the minutes…
Where did the time go? Where was the soul-crushing drudgery?
We dropped a hint when we mentioned 21 degrees and 35 minutes. There are 60 minutes in a degree, and Napier’s tables handled every degree between 0 and 90. For each of these 5400 degrees and minutes, Napier looked up its sine value from a reference, then computed the logarithm. For values close to 1 he could use the first-order Taylor approximation which is almost no work, but for most sine values he had to find the closest value in the third auxiliary table, then approximate the logarithm via the above formula for the bounds.
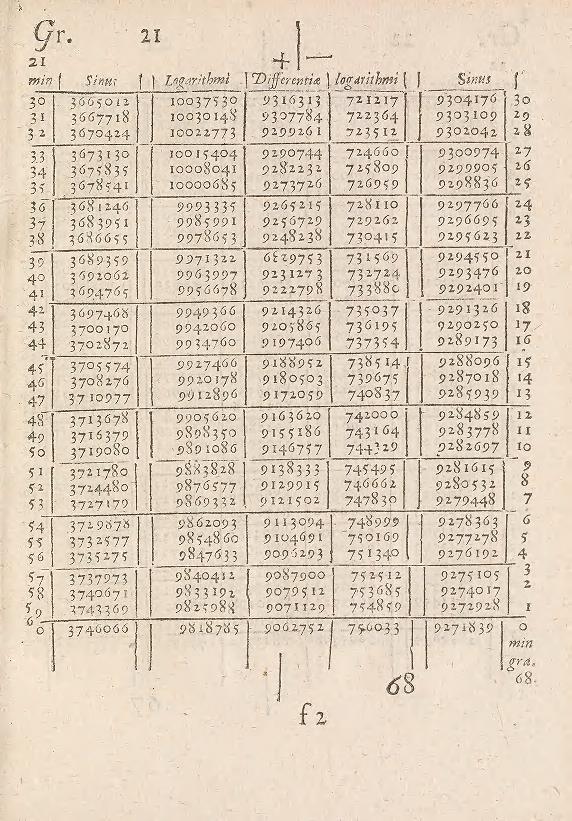
These involved divisions where geometric series approximations are of no help because the divisor is too far from 1. Some sine values required even more work, as Napier had to first apply trigonometric identities or logarithm laws to bring numbers in range of the third auxiliary table.
Napier also had to perform 2700 subtractions to compute the logarithms of tangent values. Though trivial compared to divisions, this alone is about double the number of subtractions Napier needed for the auxiliary tables.
Epilog
The obsession with precise logarithms has only intensified over the centuries. Napier gave 5 exact digits for \(\log 2\). Kepler, Newton, and Euler found 7, 16, and 25 digits, respectively.
Today, at least one trillion digits have been computed, thanks to Alexander Yee’s y-cruncher program, which uses formulas such as:
\[ \log 2 = 18 L(26) - 2 L(4801) + 8 L(8749) \]
where:
\[ L(k) = \coth^{-1}(k) = \frac{1}{2} \log \frac{k+1}{k-1} = \frac{1}{k} + \frac{1}{3k^3} + \frac{1}{5k^5} + … \]
acoth k = sum $ take 2 $ zipWith (*) denoms $ iterate ((r*r)*) r where denoms = recip <$> iterate (2+) 1.0 r = 1/k 18*acoth 26 - 2*acoth 4801 + 8*acoth 8749
Xavier Gourdon and Pascal Sebah walk through the history and the derivation of various calculation methods. My browser has trouble with their HTML so I recommend the Postscript version linked at the top of their page.