Face Detection

In order to segment human skin regions from non-skin regions based on color, we need a reliable skin color model that is adaptable to people of different skin colors and to different lighting conditions [1]. In the following section, we will describe a model of skin color in the chromatic color space for segmenting skin.

The common RGB representation of color images is not suitable for characterizing skin-color. In the RGB space, the triple component (r, g, b) represents not only color but also luminance. Luminance may vary across a person's face due to the ambient lighting and is not a reliable measure in separating skin from non-skin region [2]. Luminance can be removed from the color representation in the chromatic color space. Chromatic colors [3], also known as "pure" colors in the absence of luminance, are defined by a normalization process shown below:

Note: Color green is redundant after the normalization because r+g+b = 1.

Chromatic colors have been effectively used to segment color images in many applications [4]. It is also well suited in this case to segment skin regions from non-skin regions. The color distribution of skin colors of different people was found to be clustered in a small area of the chromatic color space. Although skin colors of different people appear to vary over a wide range, they differ much less in color than in brightness. In other words, skin colors of different people are very close, but they differ mainly in intensities [1]. With this finding, we could proceed to develop a skin-color model in the chromatic color space.

A total of 32500 skin samples from 17 color images were used to determine the color distribution of human skin in chromatic color space. Our samples were taken from persons of different ethnicities: Asian, Caucasian and African. As the skin samples were extracted from color images, the skin samples were filtered using a low-pass filter to reduce the effect of noise in the samples. The impulse response of the low-pass filter is given by:

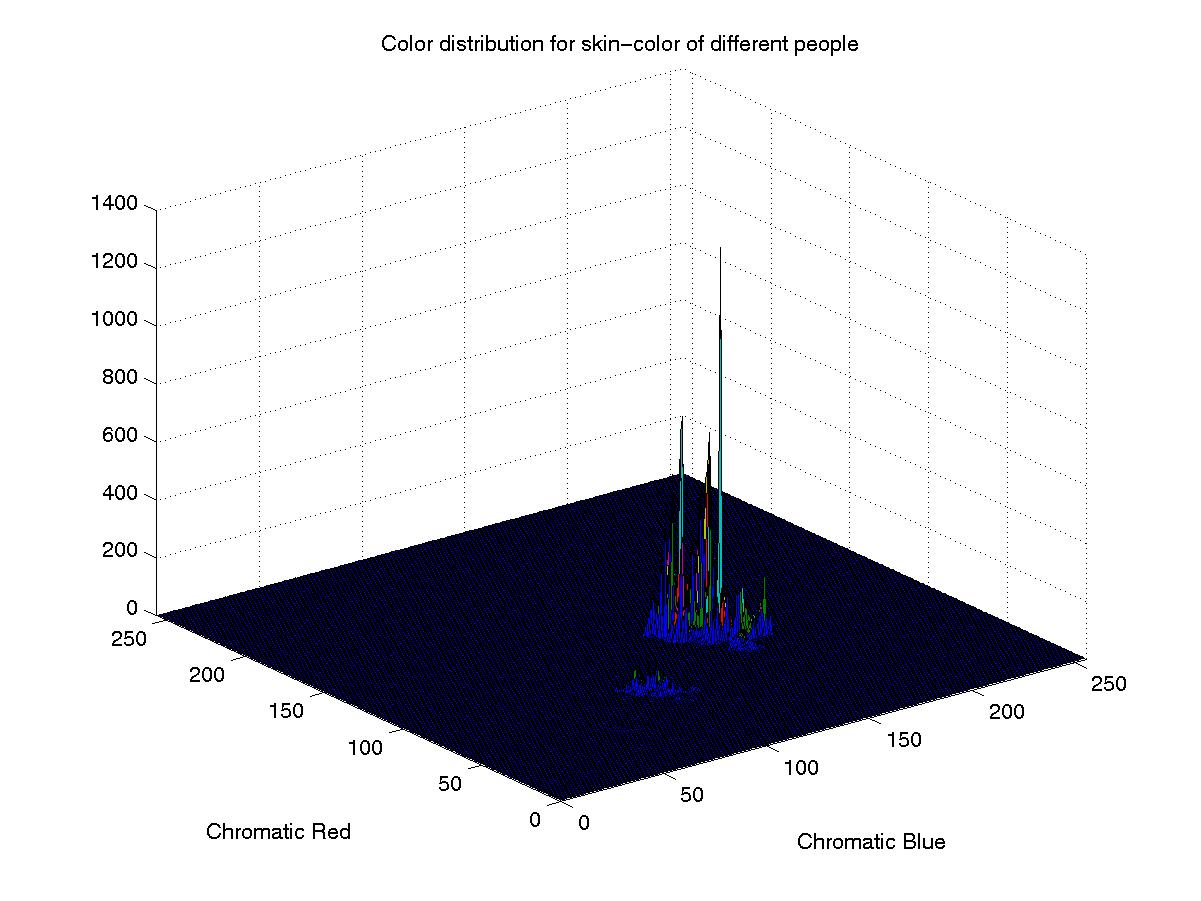
Figure 1 shows the color distribution of these skin samples in the chromatic color space.
 
 

Figure 1. Color distribution for skin-color of different people

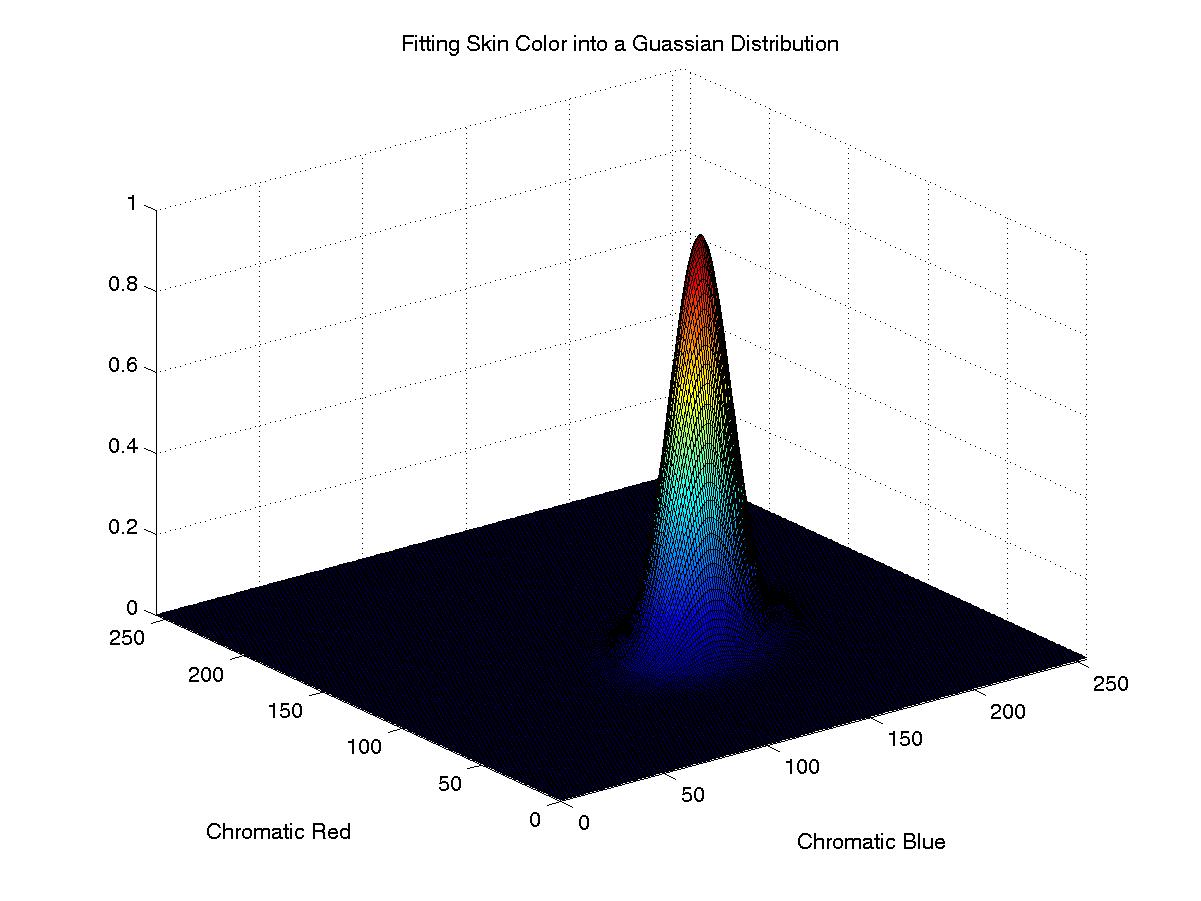
The color histogram revealed that the distribution of skin-color of different people are clustered in the chromatic color space and a skin color distribution can be represented by a Gaussian model N(m, C), where:

Figure 2. Fitting skin color into a Gaussian Distribution

With this Gaussian fitted skin color model, we can now obtain the likelihood of skin for any pixel of an image. Therefore,  if a pixel, having transform from RGB color space to chromatic color space, has a chromatic pair value of (r,b), the likelihood of skin for this pixel can then be computed as follows:

Hence, this skin color model can transform a color image into a gray scale image such that the gray value at each pixel shows the likelihood of the pixel belonging to the skin. With appropriate thresholding, the gray scale images can then be further transformed to a binary image showing skin regions and non-skin regions. This process of transforming a color image to a skin-likelihood image and then to a skin-segmented image is detailed in the next section.
 
 

Next: Skin Segmentation Previous: Introduction Contents: Face Detection