
Overview
For my CS448 project I implemented a rigid body physics engine in C#. I compute the mass properties of nonconvex polyhedra by integrating over the surface of the mesh. I use a combination of triangulated meshes and signed distance maps to dectect vertex-face intersections as well as edge-edge intersections. Collisions are resolved using impulses which are applied in three stages: an elastic collision stage to resolve collisions between moving bodiess, a more accurate contact stage to resolve the contact forces between objects in contact, and a shock-propagation stage to efficiently force contact resolution to converge. I created six demo scenes to demonstrate the physics engine at work.
Background
For my project in CS448 I implemented a rigid body physics engine based on the ideas described in the paper "Nonconvex Rigid Bodies with Stacking" (Guendelman, Bridson, and Fedkiw) (I will call this "the rigid bodies paper"). At first I had grand ideas of simulating deformable bodies - some early ideas I had were to simulate hair, a human hand, or a block of jello. All of these would have been cool, but I ended up deciding to do just a rigid body simulation instead. My first reason was curiosity: on a previous project I had worked with the Open Dynamics Engine, an open source rigid body physics engine, and I wanted write my own physics engine so I could understand some of the magic that makes physics engines tick. My second reason was interactivity: I wanted something I could play with in real time, and deformable body simulations are just a lot slower than rigid body simulations. I chose to implement the ideas from this particular paper because it seemed like a novel way of doing rigid body physics, and as it was presented in class I already had some idea of how it worked.
Platform
I decided to implement my project in Visual Studio .NET 2003, using C# and DirectX 9.0b. My main reason for doing so was because I like the C# language and I wanted to gain some experience using DirectX, as I had only used OpenGL for graphics before. In retrospect I would have been better off using C++. C# made some things a lot easier, for example loading and displaying meshes (in the DirectX format) is very easy, and the DirectX 9 managed library provides a lot of useful objects like vectors and 4x4 matrices. Unfortunately, it also made some things harder. In particular, I had a lot of problems dealing with the fact that DirectX does all linear algebra transposed from the way it is usually done. Not only did this make converting mathematical equations into code difficult, it was also quite hard for me to debug because I am so used to doing linear algebra the other way. In my frustration, I ended up writing my own matrix class to do linear algebra the usual way.
The other problem I came to realize with C# and DirectX 9.0b is simply that they are new. As a result, the documentation isn't as good, there are fewer examples available on the web, and there are not nearly as many libraries available as there would be for C++ and OpenGL. For instance, while doing this project I discovered the Magic Software site, which provides lots of free, well written C++ code that is useful in writing graphics software. I used some Magic Software code in my physics engine, and gladly have used more of their library if only it didn't take so much time to port the code to C#.
With regard to speed - a big concern when writing something like a physics engine - I found C# to be fast enough for my needs. Of course, without porting my engine to C++ I can make no concrete statements about the speed of C# compared to that of C++. However, I can state that there are many many more optimizations I could incorporate into my engine within the C# framework before I would have to move to C++ to gain any performance.
With regard to C#, my conclusion is that it would be a fine language to use to write something like a physics engine were there as many resources available for C# as for C++.
Mass Properties
The first step in a rigid body physics simulation is determining the mass properties (center of mass, total mass, and the 3x3 inertia tensor) of each body. For polyhedra of uniform density, this is a solved problem. The algorithm is described in "Fast and Accurate Computation of Polyhedral Mass Properties" (Brian Mirtich). All I did was translate the code provided with this paper from C to C#.
Collision Detection
The second step in rigid body physics is collision detection, i.e. detecting when two things hit each other. As this is often the most computationally expensive part of a physics engine, there is a lot of ongoing research into how to make collision detection as fast as possible. There are two main problems in collision detection: macro- and micro-collision detection. Macro collision detection attempts to determine which objects are "near" each other so that more expensive checks can be made to determine if they are actually in contact. Micro collision detection determines whether two objects actually are intersecting and, if so, exactly how.
I find the subject of collision detection fascinating, and before I began implementing this physics engine I spent a lot of time idly reading about and thinking about the best way to do rigid body collision detection. However, I decided to focus on collision response before spending too much time on collision detection so that I could actually simulate something. As a result I have not done nearly as much as I would like to with collision detection in my engine.
Micro Collision Detection: Triangulated Surfaces and Signed Distance Maps
For micro collision detection I do essentially the same thing as described in the rigid bodies paper: for a given body I define a signed distance map (SDM) representing the distance from any point in space to the surface of the body, and then do collision detection by checking sample points on the surface of one object against the SDM of the other body.
I store the signed distance map as a regular grid within the bounding box of each body. I considered storing the grid as an octree, but for small objects a grid is more efficient. Given a triangulated mesh representing the surface of a body, I compute the value at a particular location in the grid as the minimum over all triangles in the mesh of the distance from the point to the triangle. To this end I adapted Magic Software's point-triangle distance code. This alone would only give a distance map, however; to make it a signed distance map we need to label grid points inside the body by making their values negative.
But how to efficiently determine whether a point is inside or outside a body? I struggled with this for quite some time. My first idea was to use the dot product between the normal of the closest triangle and vector from the triangle to the point; if this dot product was negative, the point should be inside the mesh. However, this doesn't always work if the the closest point on the surface of the mesh is an edge or vertex, because then there are multiple triangles that are the same distance away, and some of them would give the correct answer and others might not. In particular, only if a triangle can be "seen" (not hidden by another triangle) from the point in question would its normal give the correct answer. Well, I didn't want to have to explicity z-sort triangles for this seemingly simple operation, so I came up with a way I thought would determine the right triangle: use the magnitude of the same dot product we computed earlier to get the distance, and take the triangle for whom this magnitude is greatest. On paper this would seem to give the right answer. Unfortunately when I coded it up I ran into numerical inaccuracies that led to "leakage" (points outside the mesh were labeled as being inside the mesh).
My second idea was to continue doing the same thing, but instead of using the exact normal from the closests triangle, use the interpolated normal instead, where the interpolated normal is what is often used to do smooth shading on triangulated surfaces. The nice thing about the interpolated normal is that it varies smoothly across the whole surface of a mesh, even when crossing edges and vertices between triangles (which were the problem cases before). I precompute the interpolated normal at each vertex as the weighted average of the normals of all adjoining faces, where the weight for a particular face is porportional to the angle subtended by that face with respect to the vertex in question (I worked this out myself, so although I can't prove it I'm pretty sure it's the right way to compute the interpolated normal; anyways it works). Then I use the point-triangle distance code to compute the barycentric coordinates of the point on the triangle closest to the point in question, and use these coordinates to interpolate the normal between the vertices of the triangle. This method worked well. (NOTE: Nathan Bell has since given me a pointer to a paper on "Generating Signed Distance Fields From Triangle Meshes" which proves that the method I came up with is valid)
Two things of note. First, unlike the rigid bodies paper, I do not initialize points near the surface and use a quick marching algorithm to intialize the rest, instead I simply initialize all points using the method described above. Thus my method would not scale well to objects with a large number of triangles. Second, because the initialization of any point in the grid is independent of any other point, this initialization can be done on demand in a lazy manner. So not until the value at a particular grid point is needed is it calculated and stored in the grid. This has two advantages, namely that it amortizes the cost of initializing the grid over each collision instead of doing it all at once when the simulation loads, and that grid points that are never needed (e.g. points well inside bodies) are never initialized.
While playing with different methods of computing the SDM, I wrote a little tool to help me visualize the SDM and its gradient. Basically it allows the user to view a single slice out of the SDM of a particular object, and the slice can be moved around.

A visualization of the discretize SDM for a tetrahedron - notice the way the corners are not sharp - this is due to discretization
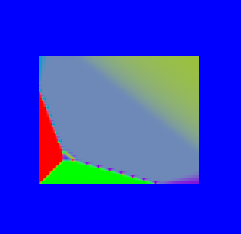
A visualization of the gradient of the same SDM - here the dicretization is even more noticeable
Surface sample points are taken from the set of vertices in the mesh representing the body, and regularly spaced points along each edge in the mesh (this allows for edge-edge intersection tests). Now, when two bodies collide, looking every one of these sample points up in the SDM of the other will be slow for large meshes. In the rigid bodies paper this is accelerated using an internal box hierachy. I did not implement this.
Macro Collision Detection: Bounding Spheres
At first I did no macro collision detection - I simply did full micro collision detection between every pair of objects. This was unbearably slow for more than a few simple objects, so as a small optimization I keep a bounding sphere around each body and check if these bounding spheres intersect before doing more expensive checks. While this suffices for a small number of relatively spherical objects, there are a number of ways I would like to imrpove this. One way would be using oriented bounding boxes to bound objects rather than spheres, perhaps integrated with an internal oriented bounding box hierarchy. Another way would be to use spatial hashing (here's a cool paper I found on the topic) to reduce the number of macro comparisons that need be made from O(n^2) to O(n), where n is the number of objects.
Collision Response
The third step in rigid body physics is collision response - what to do with two bodies once you've determine they've collided. The algorithm I implemented is pretty much straight out of the rigid bodies paper, so I won't describe it here. Suffice to say I implemented everything in sections 5-8, which includes collision modelling, static and kinetic friction, building the contact graph, contact resolution, and shock propogation. Translating the algorithm into code did not take that long, but tweaking and bug fixing did.
I only did collision processing at first - no contact or shock propogation - and made sure the code for generating and applying impulses worked before I moved on to the later parts. I quickly had something that modelled physics of some sort - not exactly plausible physics - but things were bouncing around. Then I went through the code line by line, stepping through the simulation and doing the math alongside to make sure I understood everything that was going on and looking for any errors (this was where I got frustrated with DirectX's transposed matrix math and ended up rewriting all my code using my own matrix class). One by one I found the bugs and fixed them, and each time the simulation did something different, but it wasn't necessarily getting any more plausible - I was getting discouraged after a while. Physics code is really hard to debug. Finally I fixed one major bug and things started looking a lot better. After that, bug fixing and tweaking was mostly just dealing with special cases.
Once my collisions looked good I went about optimizing the collision code to make it a bit faster, and then it was time to write the contact and shock propogation code. This went relatively fast as I was able to reuse much of the collision code. Once again there was some bug fixing and tweaking involved, but not nearly as much as before.
Demo Scenes
In order to test the various aspects of the engine, as well as to show off its capabilities, I created six demo scenes.
Stacking Scene
In this scene I let a bunch of boxes fall into a stack on top of a platform, and, just for fun, after a couple seconds another box comes flying from the left to knock the stack over. The point of this scene is to show off shock propagation: with it on, the stack is stable, but turn it off and blocks sink into each other.

With shock propagation - stack is stable

Without shock propgation - stack is unstable, bottom block sinks into platform

Gratuitous stack destruction
Tower Scene
In this scene I stack a bunch of boxes onto a stationary platform so that they form a leaning tower. This scene demonstrates a problem with shock propagation. Note that it looks like the tower should fall over, however, with shock propagation turned on it doesn't fall. If shock propagation is turned off, then the tower falls over like it should. Shock propagation is meant to help efficiently stabilize stacks, but here we see that it does so with some loss of accuracy.

With shock propagation - tower doesn't fall like it should

Without shock propagation - tower correctly falls
Sliding Scene
This scene has a very bouncy but sticky block resting on an inclined platform, and is meant to show off the unique timestepping and contact processing. If collision modeling is done before the velocity update and contact processing and shock propagation are on, then the block stays in place due to friction (as it should). If contact processing and shock propagation are turned off, the block starts to sink through the platform. If collision modeling is placed *after* the velocity update, then the block begins to vibrate and bounce down the incline.

With collision before velocity update, contact shock propagation turned on - block stays in place

With collision before velocity update, but contact and shock propagation turned off - block sinks into ground

With collision after velocity update - block bounces down the platform incorrectly
Launch Scene
This scene stacks a bunch of small blocks on a plank on top of a stationary large box, and then lets another large box fall to hit the plank and launch the smaller boxes into the air. If shock propagation is turned off then the plank begins to penetrate the box beneath it when the launch occurs.

Before the launch
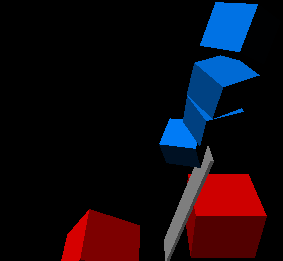
After the launch (with shock propagation on)

After the launch with shock propagation off - notice the intersection between the plank and the stationary block due to the large forces it experiences (ok, ok, if we really want to be realistic here this plank should probably break, but we're modeling *rigid* body physics here - things don't break!)
Seesaw Scene
This scene places two blocks, one large and one small, on opposite ends of a seesaw. The larger box tips the seesaw one way, then slides off, allowing the smaller box to tip the seesaw back the other way. This one is meant to show why contact processing is needed in addition to shock propagation: turn off contact processing and the seesaw fails to tip back the other way.

Seesaw at beginning of scene

After the heavy block tips it one way

After the heavy block tips the other way and slides off, with contact turned on, seesaw correctly tilts back the other way

After the heavy block tips the other way and slides off, with contact turned *off*, seesaw doesn't tilt back the other way like it should
Skull Scene
This scene has a skull and a brain falling onto a platform. It is meant to show that the engine handle arbitrary polyhedra (the skull mesh is not even a closed surface) and simulate them realistically. It runs a bit slow, especially if any more objects are added, due to the unoptimized collision detection. But it looks pretty realistic (well, if you look carefully you'll notice the brain isn't deforming as it should when it collides with the skull...hmmm, I'll have to look into that :-)

A skull followed by a brain
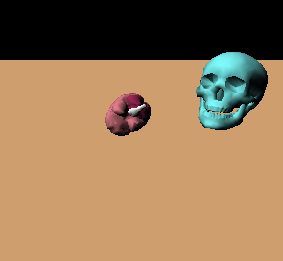
After they've bounced around a bit
Source Code and Executable
Click here to download a zip file containing the source code and executable. Run the file "run.bat" in the main directory to run the phyisics engine. You will need to have the .NET framework and DirectX 9.0b installed to run the program.
Here are the key mappings for playing with the engine:
1-6: load the corresponding demo
space bar: start/stop time
n/m: decrease/increase the number of collision iterations
j/k: decrease/increase the number of contact
p: toggle shock propagation
o: toggle whether collision modelling happens before or after the velocity update
y: turn edge-edge intersection test off
escape: exit
Cool Links
Here's a really nice implementation (much better than mine!) of some of the ideas in the rigid bodies paper: http://www.rowlhouse.co.uk/jiggle/index.html