Every year, most Cub Scout packs in the United States hold a contest they call the Pinewood Derby. Before the event, each scout and an adult helper craft a car out of a block of wood that will compete in a series of races during the event.
The race course is a sloped wooden ramp. At the top of the ramp is a wooden drawbridge that starts in the up position. Each car is placed above the drawbridge in its own lane so that the front of the car rolls to a rest touching the drawbridge. The race is started by releasing the drawbridge, letting it fall to the open position. The cars roll down the ramp. The first to reach the finish line at the bottom is the winner.
I last competed in a Pinewood Derby race some 14 years ago. My dad who helped me build the car had an electrical engineering background, and since then, I have followed in his engineering footsteps. We thought at the time that we had a marked advantage on our competitors since we theoretically knew more about how to build the car correctly. Sadly, while we did better than average in our races, we never did exceptionally.
For many years, I have wondered why our cars never performed better. Our cars were designed to be aerodynamic, in fact little more than skateboards. They tipped the weight scales at just under the allowable limit. We sanded the burrs out of the wheel wells, and added lubrication for even less friction. Still, it seemed that there was something that we missed.
One night recently, as I was lying in bed trying to fall asleep, it came to me! The more I thought about it, the more I thought I realized that I should have seen the answer much sooner. The answer lies in weight distribution.
Warning:Here comes some heavy-duty physics.
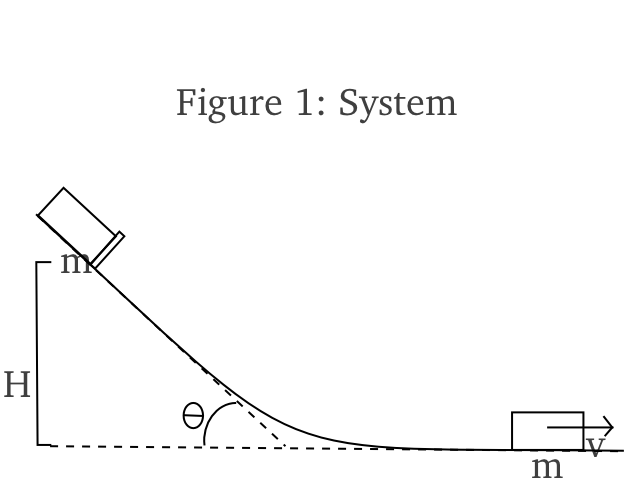
Consider the following diagram of the system:

The initial energy of the car is its potential energy relative to the end of the track.
Eo = mg(H + x sin(theta) + y cos(theta));
The end energy of the car is equal to its potential energy relative to the end of the track, plus it's kinetic energy.
Ef = mgy + 0.5 mv^2
The initial energy of the system equals the final energy of the system:
Eo = Ef
mg(H + x sin(theta) + y cos(theta)) = mgy + 1/2 mv^2
mg(H + x sin(theta) - y (1-cos(theta))) = 1/2 mv^2
v = (2g(H + x sin(theta) - y (1 - cos(theta))))^1/2
We have now solved for the final velocity of the car based on the properties of the ramp, and the properties of the car. It is important to note that this equation does not depend on the mass of the car, but it does depend on the location of the center of mass of the car relative to the dimensions of the car.
Given that the physical properties of the ramp, such as it's height and angle of inclination, are the same for all cars in the race, there is no advantage to be gained by altering the ramp (never mind the fact that the pack leader would never allow it). This leaves us to consider the changes we can make in our own car, that is, the location of the center of mass.
Our equation can be simplified by writing it as:
v = (C0 + C1 * x - C2 * y)^1/2
where:
C0 = 2gH
C1 = 2g sin(theta)
C2 = 2g (1 - cos(theta))
If we look at this equation, we can see that v gets larger as x gets larger, but that v gets smaller as y gets larger. The place in the car where the x is large and the y is small is the bottom back corner of the car.
Bottom line: Centering the weight of your car as much as possible toward the bottom, back corner of your car will make it faster during the race.
Now, I know a lot of folks out there are somewhat skeptical of this whole math and physics thing. I would like to point out this page, written by a young boy scout for a science fair project, where he does an experiment that shows empyrically that having the center of mass in the back of the car produces faster cars. Good luck building.